TEMA	GRAFICOS EN INVESTIGACION.
TIEMPO APROXIMADO	45 MINUTOS.
CURSO	CURSO METODO DE INVESTIGACION Y BIOESTADÍSTICA.
INSTRUCTOR	DR. BENJAMIN MARTINEZ R.última actualización septiembre 2021

• I. Racional.
• II. Objetivos Terminales.
• III. Objetivos Específicos
• IV. Test Inicial.
• Ciclo de Práctica I.
• Ciclo de Práctica II
• Ciclo de Práctica III
• Ciclo de Práctica IV
• V. Test Final.

---

I. RACIONAL:

Al iniciar el estudio de nuestros datos en una investigación debemos empezar por graficarlos ya que esto nos permite demostrar:

• si existe normalidad
• como se distribuyen
• si existen valores alejados o muy alejados del promedio
• si existen algunas relaciones entre ellos.

En esta unidad esperamos que conozca los principales gráficos para lograr dichos objetivos.

II. OBJETIVOS TERMINALES:

El alumno podrá:

Conocer algunos tipos de gráficos útiles para publicaciones científicas e intepretar algunos de ellos. Podrá determinar la utilidad de distintos tipos de gráficos.

III. OBJETIVOS ESPECIFICOS:

El alumno estará capacitado para:

1. Determinar qué tipos de gráficos son más adecuados para la presentación de sus resultados.
2. Interpretar diversos tipos de gráficos, tales como de barras, histograma,pie, cajas, plot y splom.
3. Conocer algunos softwares compuatacionales que le permitirán realizar dichos gráficos.

---

CICLO DE PRACTICA I:

Generalidades

Normalmente en la sección de resultados de una publicación científica debemos incluir algún tipo de gráfico que ilustre en forma clara nuestros principales hallazgos. Un gráficono sólo debe ser agradable a la vista, sino que también debe ser sencillo y autoexplicativo, y reflejar lo más fielmente posible los hechos. Es bien sabido que un gráfico dice más que muchas palabras y permite en forma clara establecer una relación o cuantificar el grado de diferencia entre dos grupos, o alguna otra relación de acuerdo a nuestros datos. Hoy en día, con la ayuda de algunos softwares computacionales tales como: Systat, Excel, STATA, SAS Minitab etc, es relativamente fácil realizar gráficos de:

• torta («pie»),
• barras,
• histogramas,
• cajas,
• tallo y hoja,
• plots, y
• splom.

Siempre debe pensar si vale la pena colocar un gráfico o si será mejor colocar una frase que simplifique más las cosas. ¨¿No será que a veces nos encontramos con gráficos para llenar espacio, o quizás para impresionar?

El tipo de gráfico que podemos realizar está de acuerdo a los própositos y a los datos o tipo de variable (por ejemplo de una variable nominal NO puede hacer un histograma, pero de cualquier variable intervalar como por ejemplo la edad puede realizar un histograma):

1. Para mostrar distribución de frecuencia de variables nominales, ordinales o discretas, utilizamos gráficos de barras simples. Para graficar distribución de frecuencia de variables continuas o intervalares, histogramas o polígonos de frecuencia, también box plots.
2. Para mostrar relación entre variables nominales, ordinales o discretas, usamos gráficos de barras pareadas o agrupadas. Con el fin de mostrar asociación entre dos variables continuas, gráficos de correlación.
3. Para graficar la relación de una parte de la información respecto al total podemos utilizar gráficos sectoriales o barras subdivididas, independientemente de las variables.
4. Para mostrar variación conjunta de dos variables continuas usamos plots o gráficos lineales.

Según las variables que tengamos nominales u ordinales, realizamos normalmente gráficos de barras separadas y gráficos sectoriales, donde cada porción «de la torta» corresponde a una categoría. Para variables intervalares normalmente se utiliza el histograma y el gráfico de barras, que demuestran promedio y desviación standard. En cuanto a asociaciones entre variables podemos utilizar los plots.

En resumen la representación gráfica de datos nos permite o sería deseable que tengan, según Gnanadesikan, 1980:

• Capacidad descriptiva
• Versatilidad
• Orientación de los datos
• Potencial para posibles comparaciones internas
• Ayuda en focalizar la atención
• Permiten autocrítica de posibles presunciones
• Adaptabilidad para grandes volumenes de datos.

Referencias bibliográficas

1. Wainer H, Thissen D. Graphical data analysis. Ann Rev Psycol 1981;32:191-241.
2. Gnanadesikan R. Graphic data analysis: issues, tools and examples. Presentado en Ann Meet Am Assoc Adv Sci. San Francisco, 1980.
3. EIA Guidelines for Statistical Graphs.

Retroalimentación

1. ¿Qué características serían deseables que tuvieran  los gráficos?

2. ¿Qué tipos de gráficos conoce ?

---

CICLO DE PRACTICA II:

GRAFICOS SECTORIALES Y DE  BARRAS

Este tipo de gráficos fundamentalmente se utilizan para variables nominales u ordinales, en las cuales tenemos categorías que difieren en la proporción o tamaño en que se han presentado en la muestra analizada. El gráfico de torta o «pie» debe tener identificadocada sector; es muy conveniente colocar, además, el número de observaciones y la frecuencia en porcentaje, adyacente a cada categoría.

En un gráfico de barras se despliega cada barra separada por categoría, donde el alto de cada barra puede representar:

1. Cuentas de cada categoría,
2. El promedio de los casos en cada categoría,
3. El porcentaje de casos en cada categoría, o
4. Alguna otra medida o estadístico ingresado por cada categoría.

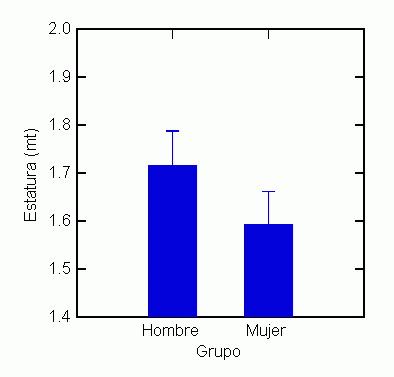
Fig. 1. Gráficos de barras. En a se presenta promedio y desviación estándar de estatura de hombres y mujeres (Dato de X. Haro). En b, se presenta promedio y desviación estándar de la edad (en años) en sexo femenino (F) y masculino (M) con desviación estándar, la cual al disminuir la intensidad del color de las barras, permite visualizar hacia arriba y abajo del promedio. Note la gran desviación estándar para cada grupo (dispersión de todos los valores: observar gráfico ).

HISTOGRAMA

Un histograma es una presentación de una distribución de frecuencia y se realiza por medio de barras o rectángulos para cada intervalo de clase, de tal forma que cada barra es proporcional a la frecuenciade cada clase. La variable intervalar es la que normalmente debe tener un histograma, el cual va a servir para demostrar la normalidad en cuanto a la distribución de la muestra examinada. Al igual que en otros tipos de gráficos el eje X debe corresponder a la variable examinada, incluyendo el valor mínimo y máximo; en el eje Y se ubica la cantidad de individuos o muestras, o sea la frecuencia. Además como cualquier gráfico debe acompañarse de un título.

No debe llamar histograma a un gráfico de barras de variables nominales u ordinales. En muchas ocasiones vemos gráficos de barras que se les denomina histogramas; en estos casos se ha ubicado en el eje Y una variable nominal u ordinal (ver Rimm, pag. 46, fig. 2), y el largo de la columna representa la frecuencia observada de cada categoría. Estos son gráficos de barra y no histogramas.

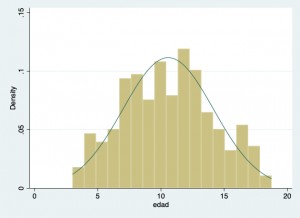
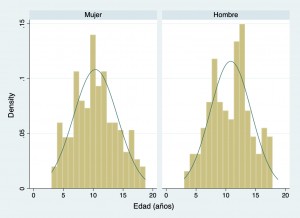
Histograma de la variable edad, realizado con Stata v. 17.  En el primero de ellos aparece para todos los niños de 3 a 18 años, y en el gráfico de más abajo, divididos entre Mujeres y Hombres. Observe que en el eje Y se presenta la densidad (proporción que representa cada barra. Además se ha trazado la campana de distribución de valores dando una idea de distribución normal.  (Datos de Daniela Estévez y Catalina Acevedo, 2021).

Referencias bibliográficas

1. Day R. Cómo preparar ilustraciones útiles, Cap. 14. en DayR. Cómo escribir y publicar trabajos científicos. Washington, OPS, Pub. científica No. 526, 1990 63.
2. Rimm AA. et al. Basic Biostatistics in medicine and epidemiology. Appleton-Century-Crofts/ New York, 1980:46.
3. Wilkinson L. SYGRAPH: the system for graphics. Evanston, IL. Systat, Inc.1990.
4. Haro X. B&uacutesqueda de un m&eacutetodo para determinar la estaturaa trav&eacutes de dimensiones craneofaciales. Trabajo de Investigaci&oacuten, Facultad de Odontolog&iacutea, U de Chile. 1997.
5. EIA Guidelines for Statistical Graphs.

Retroalimentación

1. ¿Cuál es la utilidad del gráfico de torta?

2. ¿Qué puede ir en el eje Y al realizar un gráfico debarras?

---

CICLO DE PRACTICA III

GRAFICO DE CAJAS («Box Plots»)

El plot de caja es una manera más simple que el gráficode tallo-hoja (que se explica más abajo) de desplegar datos. Esútil para identificar rápidamente la mediana, la cual esla barra al medio de la caja, barra que divide el sitio donde se encuentrala mitad de las observaciones (ver el gráfico más abajo).Los bordes de la caja o que denominaremos bisagras corresponden a los límitesque contienen la mitad de las observaciones, o sea el largo de la cajaindica donde está el 50% de los casos. Debe tenerse presente queel ancho de la caja es igual al rango medio o rango intercuartil.

Además, de cada extremo de la caja sale una línea perpendicular que contiene la distribución del resto de los casos hacia amboslados de la muestra. Las líneas perpendiculares que salen a amboslados de la caja, que llamaremos bigotes, en una distribución normaldebieran tener aproximandamente el mismo largo. Los valores que estánfuerade los bigotes son ploteados con asteriscos (*), o sea representanvaloresalejados de la distribución normal, y los valores considerablementealejados de la normalidad son representados con círculos vacíos(0).

En Systat si tenemos dos o más grupos y queremos comparar lascajas de distribución para una variable podemos utilizar estos gráficos. Cuando las cajas de dos grupos no están al mismo nivel seguramente existen diferencias significativas entre ambos grupos. Si existen variosvalores marcados con círculos vacíos es probable que la distribución en ese grupo no sea normal y a lo mejor es necesario transformar los valores.

Ejemplo:

Distribución de la edad. Gráfico de caja en base a losdatos que aparecen en el Ciclo de Práctica I. El largo de las líneas perpendiculares a la caja no es igual, o sea algunos individuos de más de 40 años, están alterando la distribución de estamuestra. Esto ocurre comunmente, no tener una distribución normal,cuando la muestra tiene menos de 20 o 30 casos. Gráfico generadocon Systat.

          BOX PLOT OF VARIABLE:     EDAD    , N =    10

23.00                                                       54.00

MINIMUM                                                     MAXIMUM

—————+——-

——+              +      +——————————-

—————+——-

Fig. 4. Gráfico de caja para la edad de los datos que se encuentran en el Ciclo de práctica II. Signo + al medio de la caja indica donde está la mediana. Realizado con Systat v.5.03.

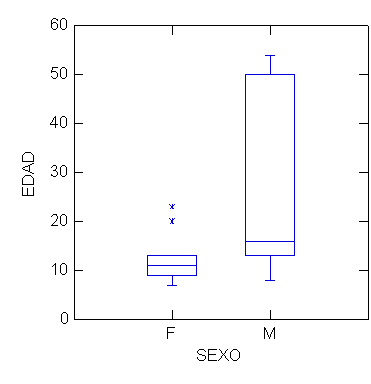
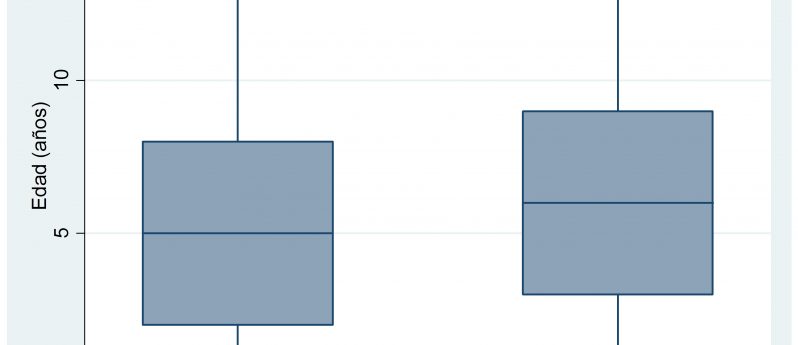
Fig. 5a.En a gráfico de cajas, para la estatura de 90 chilenos, 45 hombres y 45 mujeres, mediana entre 1.6 y 1.7 mt, y tambien note que másdel 25% mide más de 1.7 mt.  En b aparecen dos cajas, realizado con los mismos datos utilizados en la figura 1b (que aparecían con la DS). Note que el cuartil superior en las mujeres no aparece con una línea, y la mediana en el caso de los hombres no aparece al medio de la caja, indicando que las distribuciones de la edad en ambos sexos no es normal. También aparecen dos asteriscos en relación a la distribución femenina, o sea valores alejados de la distribución normal. (Gráficos realizados con Systat.

Fig. En base a recuento de cándida y el log 10, se realizó tres gráficos de caja, arriba entre grupos normal y deficientes mentales, el segundo dividiendo entre géneros femenino y masculino, y el tercero según grupos etáreos. Qué grupos presentan distribución normal ? qué grupos tenían mediana visible? Cuáles no?  Qué grupos tienen la distribución más anormal? (Gráficos realizados con Stata v. 16.1).

DIAGRAMAS DE TALLO-HOJA

Se considera el tipo de gráfico más importante para análisis de números desde que apareció el test-t. En un sentido este tipo de gráfico es una especie de presentación en barras,pero en un sentido más amplio permite el análisis de datospara examinar las propiedades de distribución de un conjunto dedatos (mediana, desviación estándar), y encontrar valoresalejados de lo normal (outside values). Todo por el precio de escribir los datos una vez y contando hacia abajo, algo parecido a un árbol, y de ahí el nombre de diagramas en Tallo-Hoja.

          STEM AND LEAF PLOT OF VARIABLE:     EDAD    , N =    10

MINIMUM:           23.00

LOWER HINGE:       27.00

MEDIAN:            34.50

UPPER HINGE:       38.00

MAXIMUM:           54.00

2   3

2 H 57

3 M 24

3 H 578

4

4   5

5   4

Fig. 7. Gráfico tallo y hoja para la distribución de las edades de 10 pacientes, arriba aparece la edad mínima, bisagra inferior (Lower hinge), o sea donde se encuentra el cuartil inferior, vale decir que está entre 23 y 27 años, después está la mediana (34,5 años), la bisagra superior (Upper hinge) de 38 años, y el valor máximo (54 años), con esos datos puede encontrar los cuartiles de la distribución de la edad.

En el gráfico de tallo-hoja anterior puede observar que la mediana es 34 años, la edad mínima es 23 años, y la máxima es 54 (datos en ciclo de práctica I). Ubique 23 y 54 años,que corresponden a los extremos de edades. La M que aparece entre dos H está indicando la ubicación de la mediana y cada H ubica los cuartiles de los casos. En este gráfico se presenta la distribución de todos los valores de la variable analizada, observe que cada valor: 23, 25,  27, 32, 34, 35, 37, 38, 45 y 54 está representado en el gráfico anterior.

Referencias bibliográficas.

1. Haro X. Búsqueda de un método para determinar la estatura a traves de dimensiones craneofaciales. Trabajo de Investigación,Facultad de Odontología, U de Chile. 1997.
2. Wilkinson L. SYGRAPH: the system for graphics. Evanston, IL. Systat, Inc.1990.
3. EIA Guidelines for Statistical Graphs.

Retroalimentación

1. En un gráfico de cajas (box plot)¿ donde se representa normalmentela mediana ?

2. ¿Qué significa las barras perpendiculares a cada lado de lacaja ?

---

CICLO DE PRACTICA IV:

GRAFICOS DE DISPERSION (PLOTS)

En el analisis de variables dependientes e independientes siempre loprimero que debe realizar, lo cual es relativamente fácil en laactualidadcon los softwares existentes, incluídas las planillasde cálculo, es la representación gráfica de los datos,ver como se distribuyen los pares de observaciones, lo cual nos va a permitirdeterminar ya visualmente si existe algún tipo de asociaciónentre las variables en estudio. Recuerde que en el eje X se ubica la variableindependiente, y en el eje Y la variable dependiente. Se puede plotearno solo variables intervalares (X e Y, intervalares), si no tambiénpuede plotear una variable categórica en el eje X vs. una intervalarlo que nos permite visualizar como se distribuyen los casos para cada grupo.

SPLOM

Un tipo muy útil es el SPLOM, gráfico que nos permiteanalizar múltiples variables intervalares, y combinar histograma,cajas u otros con gráfico de dispersión y en estos últimosal igual que en cualquier plot podemos observar la línea que definela ecuación y=a+bx, y además incluirla dispersión de la curva con un nivel de confianza, normalmentede 95%, pero que podemos modificar de acuerdo a nuestra utilidad o conveniencia.

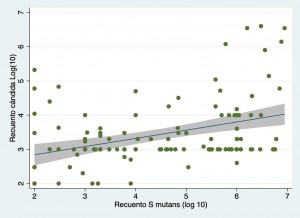
Fig. 10. Relación de recuento de cándida (log 10) vs. recuento de s mutans (log 10), datos de Dr. Alfredo Linossier.

Existen otros tipos de gráficos que nos permiten visualizar el comportamiento de varias variables, y además muchos de los gráficos quehemos mostrado como el de barras, sectoriales, pueden presentarse en formatridimensional. En la Fig. 9 tenemos una relación enzimática,gráfico proporcionado por Systat, y realizado con la versión7, que incluso permite aprovechando las bondades de la computaciónver mediante movimiento la variación experimentada.

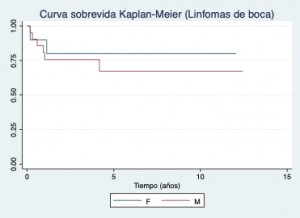
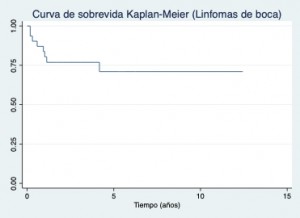
En análisis de sobrevida se utiliza la curva de Kaplan-Meier. Se muestran gráficos de sobrevida en Linfomas de boca, primero en general, y más abajo dividido en hombres y mujeres, como se observa a los cinco años tienen mejor sobreviva las mujeres.

Referencias bibliográficas.

1. Haro X. Búsqueda de un método para determinar la estatura a través de dimensiones craneofaciales. Trabajo de Investigación, Facultad de Odontología, U de Chile. 1997.
2. Wilkinson L. SYGRAPH: the system for graphics. Evanston, IL. Systat, Inc.1990.
3. EIA Guidelines for Statistical Graphs.

Retroalimentación

1. ¿Qué utilidad tienen los SPLOM ?

2. ¿Qué combinación de gráficos podría utilizaren un SPLOM ?

---

Test Final