ANALISIS DE VARIANZA – ANOVA
ANALISIS DE VARIANZA DE UNA VIA
INTRODUCCION
ANOVA, del inglés ANalysis Of VAriance, es un test estadístico ideado por Fisher, gran genio inglés que pensó hace más de 60 años como analizar datos simultáneamente cuando tenemos varios grupos y así poder ahorrar tiempo y dinero. Este análisis por lo tanto permite comprobar si existen diferencias entre promedios de tres o más tratamientos y para ello se calcula el valor de F, y es equivalente al test de Student, salvo que éste último solamente sirve para dos grupos. El problema que desde ya tenemos que dejar establecido que cuando encontramos el valor de F sabremos si existen diferencias entre los grupos, pero no no nos dice entre cuales grupos, y por eso debemos aplicar posteriormente otros tests (en inglés «post hoc tests»).
Iniciamos también con un ejemplo:
Datos: 4 tratamientos (A, B, C, D) con 3 replicas (ubicados en tres filas) y los valores para el grupo A son 5, 6 y 7 (los valores adyacentes a dicho grupo son los valores al cuadrado, para obtener la sumatoria de los cuadrados, igual para los grupos B, C y D).
|
A |
x2 |
B |
x2 |
C |
x2 |
D |
x2 |
|
5 |
25 |
5 |
25 |
4 |
16 |
6 |
36 |
|
6 |
36 |
4 |
16 |
5 |
25 |
4 |
16 |
|
7 |
49 |
5 |
25 |
3 |
9 |
6 |
36 |
|
Σx = 18 |
Σx2 = 110 |
Σx = 14 |
Σx2 = 66 |
Σx = 12 |
Σx2 = 50 |
Σx = 16 |
Σx2 = 88 |
f = 3, k = 4, n = 12
Debemos calcular:
1. Suma total de los cuadrados (STC):
STC = 14
2. Suma de cuadrados dentro de los grupos (en inglés: «within sum of squares» WSS):
WSS = 7,34
3. Suma de cuadrados entre los grupos (between sum of squares (BSS):
BSS = 6,66
4. Construcción de la tabla de Análisis de Varianza:
| Fuente de Variación | Suma de Cuadrados (SS) | grados de libertad (gl) | Cuadrado medio (MS) | Valor de F |
| Entre (Between) | 6,66 | 3 | 2,22 | 2,42 |
| Dentro (Within) | 7,34 | 8 | 0,918 | |
| Total | 14,0 | 11 |
De la tabla de valores F, Tabla 1, F,05 = 4,07
el valor obtenido, con sus grados de libertad, es F3,8 = 2,42, qué hacemos con la hipótesis nula?
Resultados con Systat
Analysis of Variance
Source Sum-of-Squares df Mean-Square F-ratio P
GRUPO 6.667 3 2.222 2.424 0.141
Error 7.333 8 0.917
————————————————————————-
Least squares means.
LS Mean SE N
GRUPO$ =A 6.000 0.553 3
GRUPO$ =B 4.667 0.553 3
GRUPO$ =C 4.000 0.553 3
GRUPO$ =D 5.333 0.553 3
Cómo graficamos tres grupos analizados con Anova de una vía ?
ANOVA; ANALISIS DE VARIANZA DE UNA VIA
COMPARACION DE MEDIAS.
TESTS DE SCHEFFÉ Y TUKEY.
Datos: 3 tratamientos con replicas (n) DIFERENTES en cada grupo.
(valor adyacente a cada columna es el valor al cuadrado, para facilitar cálculos.
1 2 3
1,0 1 4,5 20,25 1,5 2,25
3,0 9 6,0 36 -2,5 6,25
-1,0 1 3,5 12,25 -0,5 0,25
1,5 2,25 7,5 56,25 1,0 1
0,5 0,25 7,0 49 0,5 0,25
3,5 12,25 6,0 36 5,5 30,25
åx = 8,5 åx 2=25,5 40 240 0 10
x = 1,4166 5,7143 0
f= 6,7,5 k = 3, n = 18
1. Suma total de los cuadrados (SSC):
STC = åx2 – ( åx)2/n Factor de corrección (CF): (å x)2/n
STC = (25,75 + 240 + 10) – (8,5 + 40 + 0)2 /18
STC = 275,75 – 130,68
STC = 145,07
2. Suma de cuadrados dentro de los grupos (within)
- WSS = åx2 -(åxk)2/nf
- WSS = 275,75 – ( 8,52/6 + 402/7 + 02 /5)
WSS = 275,75 – ( 12,0416 + 228,57 )
WSS = 35,1384
3. Suma de cuadrados entre los grupos (between)
- BSS = (åxk )2/nf – CF
- BSS = ( 8,52/6 + 402/7 + 02/5 ) – ( 48,5) 2 /18
BSS = 12,0416 + 228,57 – 130,68
BSS = 109,931
4. Construcción de la tabla de Análisis de Varianza:
| Fuente de Variación | Suma de Cuadrados (SS) | grados de libertad (gl) | Cuadrado medio (MS) | Valor de F |
| Entre (Between) | 109,93 | 2 | 54,965 | 23,46 |
| Dentro (Within) | 35,14 | 15 | 2,3426 | |
| Total | 145,07 | 17 |
Cálculo de los grados de libertad:
gl between = número de grupos – 1
gl total = número de casos – 1
gl within = gl total – gl between
MS between = SSbetween. / glbetween.
MS within = SSwithin./glwithin.
Valor F = MSbetween. /MSwithin.
F críticos, de la tabla 1: F2,15;0.01 = 6,36 F2,15;0.005 = 7,70 por lo tanto: p<0,005
Matriz de Diferencias de los promedios de grupos:
1 2
2 4,2976
3 -1,41667 -5,71429
(Nota: diferencia del promedio del grupo 1 – promedio del grupo 2 =4,2976).
Teste de Scheffé:
Dos promedios presentan diferencias significativas si su diferencia excede el valor calculado por:
[(k-1)F0,05] 1/2[(1/n1 + 1/n2)S02 ]1/2 k = número de promedios.
F2,15;0.05 = 3,68 (valor crítico obtenido de la tabla de valores de F)
S02 = 2,3424 (de cuadrado medio, within)
Comparación diferencias de x valorde Scheffé Dif. para ser significativa
1 vs. 2 4,2976 [(2)3,68]1/2[ (1/6 + 1/7)2,3424]1/2 = 2,310
1 vs. 3 1,4116 [(2)3,68]1/2[ (1/6 + 1/5)2,3424]1/2 = 2,5142
2 vs. 3 5,714 [(2)3,68]1/2[ (1/7 + 1/5)2,3424]1/2 = 2,4312
No hay diferencias significativas entre grupos 1 vs. 3. Las otras dos comparaciones son significativas con este test de Scheffé.
Test de Tukey
Tukey = (yi -y1) ± T Ö mse
Donde T es
T = 1/ Ö n * qk, n-k,1- a= 1/ Ö 6 (3,01) = 1,2288
El valor de q (en este caso 3,01) se obtiene de tabla devalores para el test de Tukey. Al hacer estos cálculos con software estadístico, se obtiene los valores de p y debe solamente fijarse cuales son menores de 0,05 para considerarlos significativos, o menor según la significancia que ud. haya establecido.
T = 1,2288 * Ö 2,34246
T = 1,2288 * 1,5305
Del ejemplo anterior teníamos que la diferencia entre los grupos 1 vs 2 era de 4,2976 por lo tanto obtenemos:
4,2976 ± 1,8806
y esta expresión al no contener 0 hay diferencia significativaentre grupos 1 y 2 (p<0,05).
Cuando utilizar el test de Tukey ó el test de Scheffé?
Utilizar Tukey:
- Cuando el tamaño de las muestras seleccionadas para cada grupo son iguales.
- Cuando el interés fundamental es comparar promedios entre dos gruposy son múltiples las comparaciones que estamos haciendo. Por lo tanto este test de Tukey es el más utilizado, y al parecer, el más recomendado por los estadísticos, aunque al parecer aún nohay acuerdo.
Utilizar Scheffé:
- El tamaño de los grupos seleccionados es diferente (ó seaen el ejemplo anterior era mejorr este test), y
- Otras comparaciones, más que las simples comparaciones de dos promedios son de interés. A este tipo de comparaciones se les llama también contrastes.
Resultados con Systat
Effects coding used for categorical variables in model.
Categorical values encountered during processing are:
GRUPO (3 levels)
1, 2, 3
Dep Var: VALOR N: 18 Multiple R: 0.871 Squared multiple R: 0.758
Analysis of Variance
Source Sum-of-Squares df Mean-Square F-ratio P
GRUPO 109.933 2 54.966 23.465 0.000
Error 35.137 15 2.342
——————————————————————————
Note que la fuente de variación entre los grupos se denomina en estos resultados con el nombre de GRUPO, que identifica a cada categoría analizada, 3 grupos en este caso lo que da 2 grados de libertad (df, delinglés degree of freedom), y también que la fuente de variación dentro de los grupos se denomina Error.
COL/
ROW GRUPO
1 1
2 2
3 3
Using least squares means.
Post Hoc test of VALOR
——————————————————————————-
Using model MSE of 2.342 with 15 df.
Matrix of pairwise mean differences:
1 2 3
1 0.000
2 4.298 0.000
3 -1.417 -5.714 0.000
Tukey HSD Multiple Comparisons. Test de Tukey
Matrix of pairwise comparison probabilities:
1 2 3
1 1.000
2 0.000 1.000
3 0.306 0.000 1.000
——————————————————————————-
Using model MSE of 2.342 with 15 df.
Matrix of pairwise mean differences:
1 2 3
1 0.000
2 4.298 0.000
3 -1.417 -5.714 0.000
Scheffe Test.
Matrix of pairwise comparison probabilities:
1 2 3
1 1.000
2 0.001 1.000
3 0.338 0.000 1.000
——————————————————————————-
Tanto con Scheffé como con Tukey se encuentran diferencias significativas al comparar grupos 1 vs 2, y 2 vs 3; pero no existían diferencias entre los grupos 1 vs. 3. Analice porqué?
Gráficos en Anova.
Cajas para los tres grupos. Interprete los resultados obtenidos y su relación con el gráfico. Más o menos las cajas de los grupos 1 y 3 están a la misma altura, Por qué?
Gráficos con Systat (lamentablemente no se ha renovado este software, desde hace varios años).

Gráficos con Stata v. 16.1. Actualizado al 2021.


Fig. Gráficos de caja, realizados con stata v. 16.1, de Recuento de cándida (log 10) en dos grupos (Deficientes mentales y normales), y más abajo los dos grupos se subdivideron por género. Fíjese que en algunas cajas no aparece la mediana, además varios valores se alejan de la distribución normal. En cuál de esos tres gráficos utilizaría Anova?
Referencias bibliográficas.
- Kleinbaum DG, Kupper LL. Applied regression analysis and other multivariable methods. Duxbury Press, North Scituate, MA, USA, 1978.
ANALISIS DE VARIANZA DE DOS VIAS
En los ejemplos anteriores teníamos un solo factor, pero muchas veces podemos analizar simultáneamente más de uno, por ejemplo puede interesararnos si existe diferencias entre hombres y mujeres (factor 1), y nivel socioeconómico (alto, medio y bajo), en el COPD, deniños que hemos seleccionado de la región metropolitana.
Plantee un problema con dos factores:
Cómo analizar estos datos? Con un ejemplo creemos siempre quese entiende mejor la estadística.
Ha sido realizado un estudio para demostrar el efecto de tres suplementos de mineral en la dieta de ratas albinas, machos y hembras. Para demostrar si dicho suplemento tiene algún efecto en el peso del riñón, el órgano fue pesado al momento de sacrificar al animal (día 90 de edad). Se evalúa si existe cambio de peso debido a los suplementos, y si existe diferencia por género.
Cuál es la hipótesis nula?
Control (1) |Alimento A |Alimento B
| |
Machos Hembras |Machos Hembras | Machos Hembras
————————– |————————– |—————————
2,30 1,62 | 2,68 1,78 | 2,57 1,67
1,31 1,43 | 2,62 1,78 | 2,97 2,47
3,03 1,48 | 2,32 1,89 | 1,37 1,65
2,45 1,49 | 2,08 1,99 | 2,47 1,72
2,22 1,44 | 2,92 1,79 | 2,85 2,02
2,10 1,41 | 2,52 1,42 | 2,97 1,97
———————————————————————————–
åx = 13,41 8,87 15,14 10,65 15,2 11,5 (sumatoria de los grupos)
åx2 = 31,53 13,14 38,63 19,09 40,35 22,53(suma de cuadrados de cada grupo)
x = 2,24 1,48 2,52 1,78 2,53 1,92 (promedio de cada grupo)
åxc = 22,28 åxa = 25,79 åxb = 26,7 (sumatoria de valores por grupo)
åxc2 = 44,67 åxa2 = 57,72 åxb2 = 62,88 (sumatoria de valores al cuadrado de cada grupo)
xc = 1,856 xa = 2,15 xb = 2,225 (promedio de cada grupo, incluye machos y hembras)
åxm = 43,75 åxh = 31,02 (sumatorias de valores en machos, y hembras)
åxm2 = 110,50 åxh2 = 54,76 (sumatorias al cuadrado de valores de machos y hembras)
xm = 2,43 xh = 1,72 (promedios en machos y hembras)
Sumatorias por filas:
åxf1 = 7,55
åxf2 = 6,9
åxf3 = 6,72
åxf4 = 7,00
åxf5 = 7,99
åxf6 = 7,59
åxf7 = 5,07
åxf8 = 5,68
åxf9 = 5,02
åxf10 = 5,2
åxf11 = 5,25
åxf12 = 4,8
n = 36, f = 6, grupos= 3, géneros = 2
1. Suma total de los cuadrados (STC):
STC = åx2 – ( åx)2/n Factor de corrección (CF): (å x)2/n
STC = (44,67+57,72+62,28) – (22,28+25,79+26,7)2 /36
STC = 164,67 -; 155,293
STC = 9,37
2. Suma de cuadrados entre los grupos de tratamiento (between):
BSS = (åx k)2/nf – CF
BSS = ( 22,282/12 +25,792/12 +26,72/12) – 155,293
BSS = 156,20 – 155,293
BSSt = 0,911
3. Suma de cuadrados entre los grupos, género (between)
BSS = (åx k)2/nf – CF
BSS = ( 7,552/3 +6,92/3 +6,722/3 +7 2/3+7,992/3+7,592/3 +5,072/3 +5,68 2/3+5,022/3+5,22/3 +5,252/3 +4,8 2/3 ) – 155,293
BSSg = 4,535
4. Suma de cuadrados subtotal:
SSt = (åxg /ng)2- CF
- =( 13,412/6 +15,142/6 +15,272/6+8,87 2/6+10,652/6 +11,52/6) – 155,29
= 5,446
5. Suma de cuadrados dentro de los grupos (within)
WSS = åx2 -(åxk)2/nf
WSS = (44,67+57,72+62,88) – 161,10
WSS = 3,89
Construcción de la tabla de Análisis de Varianza:
| Fuente de Variación | Suma de Cuadrados (SS) | grados de libertad (gl) | Cuadrado medio (MS) | Valor de F |
| Entre (Between), tratamientos | 0,911 | 2 | 0,455 | 3,273 |
| Entre (Between) géneros | 4,5 | 1 | 4,535 | 35,15 |
| Interacción | 0,037 | 2 | 0,019 | 0,698 |
| Subtotal | 5,446 | 5 | 0,918 | |
| Dentro (within) | 3,89 | 30 | 0,129 | |
| total | 9,377 | 35 |
F3,8 = 2,42, F,05 = 4,07
ANALISIS DE VARIANZA DE DOS VIAS
La extracción total de lípidos de los dientes ha sido facilitado mediante la incubación preliminar de la muestra en solución de EDTA al 15% a pH 7.4 a 38°C durante 18 hrs. En orden de demostrarsi este procedimiento pudiera mejorar la extracción de lípidos desde muestras de alimentos, se realizó un experimento con tres muestras: A. róbalo fresco, B. róbalo apanado, C. brocolifresco. Cada análisis se repitió tres veces obteniéndose los siguientes resultados:
Método I Método II
(Incubación en EDTA) (Incubación con H2O)
——————————————————————–
A 0,635 0,642 1
0,634 0,621 2
0,574 0,445 3
B 5,576 5,591 4
5,906 6,343 5
6,059 6,224 6
C 0,812 0,894 7
0,814 0,818 8
0,806 0,922 9
åx = 21,816 22,5
åx2 = 105,7903 113,5453
x = 2,424 2,5
åxa = 3,551 åxb = 35,699 åxc = 5,066
åxa2 = 2,1304 åxb2 = 212,915 åxc2 = 4,290
xa = 0,592 xb = 5,95 xc = 0,844 (Promedios de grupos a, b y c)
åxIA = 1,843
åxIB = 17,541
åxIC = 2,432
åxIIA = 1,708
åxIIB = 18,158
åxIIC = 2,634
n = 18, f = 9, grupos = 3, métodos = 2
1. Suma total de los cuadrados (STC):
STC = åx2 – ( åx)2/n Factor de corrección (CF): (å x)2/n
(21,816+22,5)2 /18 = 109,106
STC = (105,79 + 113,54) – (21,816 + 22,5)2 /36
STC = 110,230
2. Suma de cuadrados entre los métodos de tratamiento (between):
- BSS = (åxk )2/nf – CF
BSS = ( 21,8162/9 + 22,52/9 ) – 109,106
BSSt = 109,6761
3. Suma de cuadrados subtotal:
SSS = (åxg )2/ng- CF
SSS = ( 1,8432/3 + 1,7082/3 + 17,5412 /3+ 18,1582/3 + 2,4322/3 + 2,6342/3 ) – 109,106
SSS = 218,855 – 109,106
SSS = 109,74932
4. Suma de cuadrados dentro de los grupos (within)
WSS = åx2 -(åxk)2/nf
WSS = ( 105,79 + 113,5453 ) – ( 1,8432/3 + 1,708 2/3+ 17,5412/3 + 18,1582/3 + 2,4322 /3 + 2,6342/3)
WSS = 0,4803
Construcción de la tabla de Análisis de Varianza:
| Fuente de Variación | Suma de Cuadrados (SS) | grados de libertad (gl) | Cuadrado medio (MS) | Valor de F |
| Métodos | 0026 | 1 | 0,026 | 0,65 |
| Alimentos | 109,67,5 | 2 | 54,838 | 1370,95 |
| InteracciónMétodos * Alim. | 0,047 | 2 | 0,02361 | 0,5898 |
| Subtotal | 109,74 | 5 | ||
| Dentro (within) | 0,480 | 12 | 0,04002 |
F2,12,0.05 A,B,C = 3,88 F1,12,0.05 Métodos I y II = 4,75
Interpretar…
Cuáles eran las hipótesis de nulidad ?
Se aceptan ? Se rechazan ?
Análisis estadístico de dos vías, resultados conSystat.
SYSTAT Rectangular file C:\Archivos de programa\SYSTAT 8.0\ANOVA2V.SYD,
created Wed May 26, 1999 at 11:22:38, contains variables:
Categorical values encountered during processing are:
GRUPO$ (3 levels)
A, B, C
METODO$ (2 levels)
I, II
Dep Var: LIPIDOS N: 18 Multiple R: 0.998 Squared multiple R: 0.996
Analysis of Variance
Source Sum-of-Squares df Mean-Square F-ratio P
GRUPO$ 109.644 2 54.822 1372.854 0.000
METODO$ 0.027 1 0.027 0.670 0.429
GRUPO$*METODO$ 0.047 2 0.024 0.591 0.569
Error 0.479 12 0.040
——————————————————————————-
Tabla 1. Tabla de valores de F, 5%.
|
GL Num
GL Den |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 20 | ¥ |
| 1 | 161,448 | 199,50 | 215,707 | 224,583 | 230,162 | 233,986 | 236,768 | 238,883 | 240,543 | 241,882 | 248,013 | 254,314 |
| 2 | 18,5128 | 19,000 | 19,1643 | 19,2468 | 19,2964 | 19,3295 | 19,3532 | 19,3710 | 19,3848 | 19,3959 | 39,4458 | 19,4957 |
| 3 | 10,1280 | 9,5521 | 9,2766 | 9,1172 | 9,0135 | 8,9406 | 8,8867 | 8,8452 | 8,8123 | 8,7855 | 8,6602 | 8,5265 |
| 4 | 7,7086 | 6,9443 | 6,5914 | 6,3882 | 6,2561 | 6,1631 | 6,0942 | 6,04106 | 5,9988 | 5,9644 | 5,8025 | 5,6281 |
| 5 | 6,6079 | 5,7861 | 5,4095 | 5,1922 | 5,0503 | 4,9503 | 4,8759 | 4,8183 | 4,7725 | 4,7351 | 4,5581 | 4,3650 |
| 6 | 5,9874 | 5,1433 | 4,7571 | 4,5337 | 4,3874 | 4,2839 | 4,2067 | 4,1468 | 4,0990 | 4,0600 | 3,7842 | 3,6689 |
| 7 | 5,5915 | 4,7374 | 4,3468 | 4,1203 | 3,9715 | 3,8660 | 3,7870 | 3,7257 | 3,6767 | 3,6365 | 3,4445 | 3,2298 |
| 8 | 5,3177 | 4,4590 | 4,0662 | 3,8379 | 3,6875 | 3,5806 | 3,5005 | 3,4381 | 3,3881 | 3,3472 | 3,1503 | 2,9276 |
| 9 | 5,1174 | 4,2565 | 3,8625 | 3,6331 | 3,4817 | 3,3738 | 3,2927 | 3,2296 | 3,1789 | 3,1373 | 2,9365 | 2,7067 |
| 10 | 4,9646 | 4,1028 | 3,7083 | 3,4780 | 3,3258 | 3,2172 | 3,1355 | 3,0717 | 3,0204 | 2,9782 | 2,7740 | 2,5379 |
| 11 | 4,8443 | 3,9823 | 3,5874 | 3,3567 | 3,2039 | 3,0946 | 3,0123 | 2,9480 | 2,8962 | 2,8536 | 2,6464 | 2,4045 |
| 12 | 4,7472 | 3,8853 | 3,4903 | 3,2592 | 3,1059 | 2,9961 | 2,9134 | 2,8486 | 2,7964 | 2,7534 | 2,5436 | 2,2962 |
| 13 | 4,6672 | 3,8056 | 3,4105 | 3,1791 | 3,0254 | 2,9153 | 2,8321 | 2,7669 | 2,7144 | 2,6710 | 2,4589 | 2,2064 |
| 14 | 4,6001 | 3,7389 | 3,3439 | 3,1123 | 2,9582 | 2,8477 | 2,7642 | 2,6987 | 2,6458 | 2,6022 | 2,3879 | 2,1307 |
| 15 | 4,5431 | 3,6823 | 3,2874 | 3,0556 | 2,9013 | 2,7905 | 2,7066 | 2,6408 | 2,5876 | 2,5437 | 2,3275 | 2,0659 |
| 16 | 4,4940 | 3,6337 | 3,2389 | 3,0069 | 2,8524 | 2,7413 | 2,6572 | 2,5911 | 2,5377 | 2,4935 | 2,2756 | 2,0096 |
| 17 | 4,4513 | 3,5915 | 3,1968 | 2,9647 | 2,8100 | 2,6987 | 2,6143 | 2,5480 | 2,4943 | 2,4499 | 2,2304 | 1,9604 |
| 18 | 4,4139 | 3,5546 | 3,1599 | 2,9277 | 2,7729 | 2,6613 | 2,5767 | 2,5102 | 2,4563 | 2,4117 | 2,1906 | 1,9168 |
| 19 | 4,3808 | 3,5219 | 3,1274 | 2,8951 | 2,7401 | 2,6283 | 2,5435 | 2,4768 | 2,4227 | 2,3779 | 2,1555 | 1,8780 |
| 20 | 4,3512 | 3,4928 | 3,0984 | 2,8661 | 2,7109 | 2,5990 | 2,5140 | 2,4471 | 2,3928 | 2,3479 | 2,1242 | 1,8432 |
| 30 | 4,1709 | 3,3158 | 2,9223 | 2,6896 | 2,5336 | 2,4205 | 2,3343 | 2,2662 | 2,2107 | 2,1646 | 1,9317 | 1,6223 |
| 40 | 4,0847 | 3,2317 | 2,8387 | 2,6060 | 2,4495 | 2,3359 | 2,2490 | 2,1802 | 2,1240 | 2,0772 | 1,8389 | 1,5089 |
| 50 | 4,0343 | 3,1826 | 2,7900 | 2,5572 | 2,4004 | 2,2864 | 2,1992 | 2,1299 | 2,0734 | 2,0261 | 1,7841 | 1,4383 |
| 60 | 4,0012 | 3,1504 | 2,7581 | 2,5252 | 2,3683 | 2,2541 | 2,1665 | 2,0970 | 2,0401 | 1,9926 | 1,7480 | 1,3893 |
| 70 | 3,9778 | 3,1277 | 2,7355 | 2,5027 | 2,3456 | 2,2312 | 2,1435 | 2,0737 | 2,0166 | 1,9689 | 1,7223 | 1,3529 |
| 80 | 3,9604 | 3,1108 | 2,7188 | 2,4859 | 2,3287 | 2,2142 | 2,1263 | 2,0564 | 1,9991 | 1,9512 | 1,7032 | 1,3247 |
| 90 | 3,9469 | 3,0977 | 2,7058 | 2,4729 | 2,3157 | 2,2011 | 2,1131 | 2,0430 | 1,9856 | 1,9376 | 1,6883 | 1,3020 |
| 100 | 3,9361 | 3,0873 | 2,6955 | 2,4626 | 2,3053 | 2,1906 | 2,1025 | 2,0323 | 1,9748 | 1,9267 | 1,6764 | 1,2832 |
| ¥ | 3,8415 | 2,9957 | 2,6049 | 2,3719 | 2,2141 | 2,0986 | 2,0096 | 1,9384 | 1,8799 | 1,8307 | 1,5705 | 1,0023 |
Tabla tomada de: Weintrabu JA, Douglass CW, Gillings DB: «Bioestadística en salud bucodental» , OPS, 1989, Chapel Hill, NC, USA, pag:191.
ANALISIS DE VARIANZA DE MEDIDAS REPETIDAS
A veces realizamos a un mismo grupo de pacientes distintos tratamientos, o sea la variación es más importante entre los distintos tratamientos que entre los sujetos. Por ejemplo si quisiéramos determinar cuatro antibióticos que pueden bajar el nivel de s mutans en saliva,y le damos a los mismos pacientes (dejándolos descansar entre uno y otro antibiótico, déjelos que se recuperen !), cuatro antibióticos diferentes.
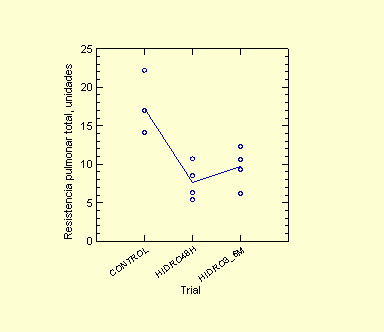
En el ejemplo que vamos a ilustrar este análisis tenemos cuatro sujetos que recibieron tres tratamientos diferentes por hipertensión pulmonar:
(hidrolacina se administró a las 48 hrs y después entre 3 y 6 meses (ahí tenemos dos grupos), el otros grupo,control, son los mismos pacientes antes del tratamiento.
Sujeto Control Hidrolacina | x SS
48 hrs 3-6 Meses |
1 22,2 5,4 10,6 | 12,73 147,95
2 17,0 6,3 6,2 | 9,83 77,05
3 14,1 8,5 9,3 | 10,63 18,35
4 17,0 10,7 12,3 | 13,33 21,45
x = 17,58 7,73 9,6 | 11,63 SS total = 289,82
Esta tabla incluye el promedio para cada grupo de tratamiento y para cada individuo con los tres tratamientos, también gran promedio de todos (11,63) y suma de cuadrados de los sujetos (289,82).
Por ejemplo SS para el sujeto 2:
SSt2 = S (S t2 – x2) 2
SS2 = (17 – 9,83)2 + (6,3 – 9,83) 2 +(6,2 – 9,83)2 = 77,05
1. La suma de cuadrados dentro de los sujetos (SSw) será :
SSw = SS1 + SS2 + SS3 + SS4
SSw = 147,95 + 77,05 +18,35 +21,45
SSw = 264,80 unidades2
2. La suma de cuadrados entre los grupos será:
SSb = m S (Ss – x) 2
SSb = 3 [(12,73 -11,63 ) 2 + (9,83 – 11,63 ) 2+ (10,63 – 11,63 ) 2 + (13,33 – 11,63 ) 2]
SSb = 25,02 unidades2
3. La suma total de los cuadrados será:
STC = SSw + SSb
STC = 264,80 + 25,02
STC = 289,82
4. Ahora calculamos SS para los tratamientos:
SSt = n S (T – x)2
SSt = 4 [(17,58 -11,63 ) 2 + (7,73 – 11,63 ) 2 + (9,60 -; 11,63 ) 2 ]
SSt = 218,93 unidades2
5. SS de los valores residuales:
SSr = SSw -SSt
SSr = 264,80 – 218,93
SSr = 45,87 unidades2
6. Con estos valores construimos la tabla de Anova
Construcción de la tabla de Análisis de Varianza:
| Fuente de Variación | Suma de Cuadrados (SS) | grados de libertad (gl) | Cuadrado medio (MS) | Valor de F |
| Entre Sujetos | 25,02 | 3 | ||
| Dentro de Sujetos
Tratamiento
Residual
|
265,80218,9345,87 | 826 | 109,477,65 | 14,31 |
| Total | 289,82 | 11 |
F2,6, 0.01 = 10,92 (F crítico de la tabla)
Resultados con Systat de Anova de medidas repetidas.
Univariate and Multivariate Repeated Measures Analysis
Within Subjects
—————
Source SS df MS F P G-G H-F
a 218.852 2 109.426 14.293 0.005 0.022 0.011
Error 45.935 6 7.656
Greenhouse-Geisser Epsilon: 0.6080
Huynh-Feldt Epsilon : 0.8028
—————————————————-
El estadístico Greenhouse-Geisser (G-G) es un valor utilizado para ajustar los grados de libertad cuando la presunción de simetría compuesta no se cumple. Por otra parte Huynh-Feldt se ajusta cuando la premisa menos restrictiva es violada. El ideal es que G-G no sea muy diferente del valor de p que está a su izquierda, y H-F debe ser parecidoa G-G, en su valor de p.
1. Cuál era la hipótesis nula ?
2. Explique los resultados.
3. Sugiera :
A. Experimento donde sea aplicable Anova de una vía.
B. Experimento donde sea aplicable Anova de dos vías (o más si quiere…).
C. Experimento donde sea aplicable Anova de medidas repetidas.


