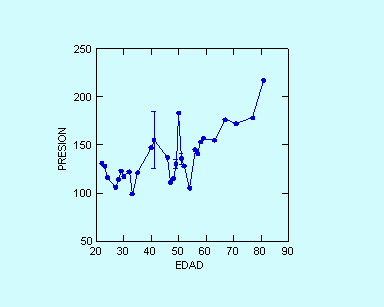
Fig. 2. Dispersión que tienen algunos valores, por ejemplo a los 41 años habían varias observaciones de presión, igualmente a los 51 años.
UNIDAD DE AUTO APRENDIZAJE
para alumnos de Odontología,
curso de Bioestadística.
ANALISIS DE REGRESIÓN SIMPLE
- CORRELACIÓN DE PEARSON
Dr. Benjamín Martínez R.
Profesor de Bioestadística
Cuando deseamos estudiar la asociación de dos variables, normalmente intervalares, y queremos establecer como varía una con respecto de la otra, y hablamos de una variable dependiente y una independiente, el test estadístico más indicado para establecer dicha asociación es el análisis de regresión simple. Como tenemos dos variables, tenemos que tener pares de observaciones, o sea parejas, y al igual que en la "relación de pareja", muchas veces interesa conocer:
Tabla 1. Edad vs. Presión sistólica en 33 pacientes.
| Edad | PS |
| 22 | 131 |
| 23 | 128 |
| 24 | 116 |
| 27 | 106 |
| 28 | 114 |
| 29 | 123 |
| 30 | 117 |
| 32 | 122 |
| 33 | 99 |
| 35 | 121 |
| 40 | 147 |
| 41 | 139 |
| 41 | 171 |
| 46 | 137 |
| 47 | 111 |
| 48 | 115 |
| 49 | 133 |
| 49 | 128 |
| 50 | 183 |
| 51 | 130 |
| 51 | 133 |
| 51 | 144 |
| 52 | 128 |
| 54 | 105 |
| 56 | 145 |
| 57 | 141 |
| 58 | 153 |
| 59 | 157 |
| 63 | 155 |
| 67 | 176 |
| 71 | 172 |
| 77 | 178 |
| 81 | 217 |
Variable dependiente: la presión sistólica
Variable independiente: la edad
n = 33 åx = 1542 (sumatoria
de las edades)
åy = 4575 (sumatoria de las presiones)
åxy = 223.144 (productos cruzados)
x = 46,73 y = 138,64 (promedio de x e y, o sea promedios de la edad y la presión)
å(y – y)2 = åy2 – (åy)2 / n = 656.48116 – (4575) 2 / 33 = 22.219,6 (idem la segunda y es el promedio).
å(x – x) (y – y) = åxy – (åx)(åy) /n = 223.144 – (1542)(4575)/33 = 9.366,7
y = a + bx
Cálculo de b ó en otras palabras la pendiente de la curva:
å(x – x) (y – y)
b = - - -- - - - - - - - - - - - - = 9366,7 / 7662,6 = 1.22 mm Hg / año
de edad
å(x – x)2
Para calcular a, se despeja de la ecuación y = a + b x, y el valor de x e y es reemplazado por los promedios:
a = y – b
x = 138,64 – (1,22)(46,73) = 81,54
y = 81,54 + 1,22 x
a: intercepto, en mm de Hg
b: pendiente, ps aumenta 1,22 mmHg por cada año de edad.

Fig. 2. Dispersión que tienen algunos valores, por ejemplo a los
41 años habían varias observaciones de presión, igualmente
a los 51 años.
åy2 – aåy – båxy
656.481 – (81,54)(4575) – (1,22)(223.144)
Sy.x = Ö
- - - - - - - - - - - - - - = Ö
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
n - 2
33 - 2
Sy.x = 18,64
S2y.x = 347,41
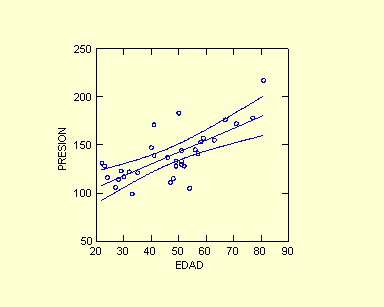
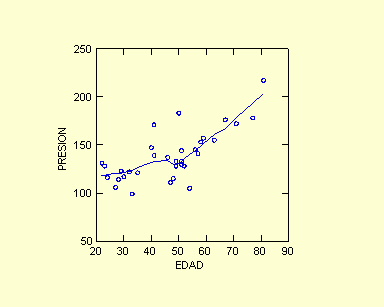
Fig. 3. Los datos se resumen con la ecuación que representa la
recta trazada en este gráfico, por lo tanto y = 81,54 + 1,22 x.
El intercepto a 81.54 no coincide siempre con lo que obtenemos en los gráficos.
Aquí vemos claramente como es la tendencia: a medida que avanza
la edad aumenta la presión sistólica.
åx2 – (åx)2
/ n
7.662,6
r = bÖ S x / S y
= 1,22 * Ö --------------
= 1,22 * Ö --------
åy2 – (åy)2
/ n
22.219,6
r = 0.71
(Este valor es la correlación de Pearson, indica la fuerza de la
asociación entre las dos variables, puede variar entre -1 y 1, y se
considera que entre más cerca de 1 mejor es la asociación de
las variables. Cuando el valor es sobre 0,65 se considera la correlación
buena, entre 0,4 y 0,649 regular, y menos de 0,4 mala)
r2 = 0.51 (El valor de r elevado al cuadrado nos entre la proporción
de varianza de la variable dependiente, en este caso de la presión
sistólica, debido al predictor, la edad).
SEb = Ö S2y.x / å(x – x)2 = Ö 347,41/7.662,6 = 0,2129
SEa = Ö S2y.x
[ 1/n + x /å(x
– x)2 ] = Ö 347,41 [ 1/33 + (46,73)2
/ 7.662,6] = 10,47
Intervalo de Confianza (95%)
b ± (t31; 0,05) (SEb) = 1,22 ± (1,96)
(0,2129)
= 1,22 ± 0,417
En la fig. 3 el intervalo de confianza al 95% se encuentra delimitado
por las dos curvas a ambos lados de la recta.
Test de significancia para la Ho de b = 0 (ó en otras palabras
de que la pendiente es 0, nos interesa demostrar si la pendiente es distinta
de 0.
b -
0
1,22
t31 = ---------------- = ----------- =
5,74 (p <0,001) Por lo tanto la pendiente es distinta
de 0.
SEb
0,2129
Interprete estos resultados y compare con los obtenidos.
¿Cómo cree que puede presentar estos resultados para una
publicación?

Fig. 4. Valores residuales del ejercicio de la relación entre presión
sistólica vs. edad.
Otro resultado, ahora con Systat v. 11 (2004). En este estudio, R Godoy (Odontología, UCH) seleccionó 65 pacientes, todos ellos tenían antecedentes de neuralgia del trigémino, y quisimos ver si existía una relación entre sus edades y el promedio de la presión sistólica (P_SISTP), la cual fue tomada en varias ocasiones. El resultado obtenido es:
1. Dep Var: P_SISTP N: 65 Multiple R: 0.337 Squared multiple R: 0.114
2. Adjusted squared multiple R: 0.100 Standard error of estimate: 21.072
|
3. Effect |
Coefficient |
Std Error |
Std Coef |
Tolerance |
t |
P(2 Tail) |
|
4. CONSTANT |
103.160 |
14.345 |
0.000 |
. |
7.192 |
0.000 |
|
5. EDAD |
0.627 |
0.220 |
0.337 |
1.000 |
2.842 |
0.006 |
6. Analysis of Variance
|
7. Source |
Sum-of-Squares |
df |
Mean-Square |
F-ratio |
P |
|
8. Regression |
3586.764 |
1 |
3586.764 |
8.077 |
0.006 |
|
9. Residual |
27974.840 |
63 |
444.045 |
10. *** WARNING ***
11. Case 3 is an outlier (Studentized Residual = 3.534)
12. Durbin-Watson D Statistic 2.174
13. First Order Autocorrelation -0.105
Los número del 1 al 13 que aparecen al principio los hemos colocado para facilitar la explicación, NO aparecen así en los listados de systat.
1. Variable dependiente: P_SISTP: variable que ingresamos como dependiente, N: 65 pacientes con los valores, Multiple R: correlación de Pearson, 0,337 (mala) (debe cambiar el signo si el valor de la pendiente b es negativo, en este caso b = 0,627, fila 5). Squared multiple R: corresponde al valor de Pearson elevado al cuadrado: 0,114 y es la proporción de la variación total de la variable dependiente que se explica por la edad (11.4%). Este valor se puede obtener de la suma de cuadrados de la tabla de análisis de varianza y es igual a : 3586.764 / (3586.764 + 27974.84).
2. Adjuested squared multiple R: tiene utilidades en modelos con más de una variable independiente. Standar error of estimate: es la raíz cuadrada del cuadrado medio residual en la tabla de anova.
3, 4 y 5. Títulos para la tabla del análisis de regresión. De donde se debe obtener los coeficientes, primera columan, para la ecuación, que en este caso es: p_sistp = 103.16 + 0.627 * edad
3, 4 y 4. Los errores estándar (Std Error) de los coeficientes estimados están en la siguiente columna, y después están los coeficientes estandarizados (Std Coef). A estos últimos se les llama también beta (algunos sicólogos o investigadores sociales). Tolerance, no es relevante cuando hay solamente un predictor. Después están los valores de t, el primero (7.192), comprueba la significancia de la diferencia de la constante de 0 (significativa en este caso, p < 0.0005), el segundo valor de t (2.842) comprueba la significancia de la pendiente, lo cual es similar a demostrar la significancia de la correlación entre edad vs p_sistp.
7, 8 y 9. El valor F (F-ratio), en la tabla de analisis de varianza es utilizado para demostrar la hipótesis que la pendiente es 0 (o en regresión múltiple, que todas las pendientes son 0). F es grande cuando la variable independiente ayuda a explicar la variación en la variable dependiente. Aquí hay una relación linear significativa entre presión sistólica y edad. Por lo tanto rechazamos la hipótesis que la pendiente de la línea de regresión es 0 (F = 8.077, p = 0.006), vale decir a medida que aumenta la edad la presión está aumentado. .
10. Advertencia :::: siempre fíjese que aparece y qué signifca esto
11. Case 3..., es de un valor anormal, al revisar los datos originales
esta era una paciente que tenía presión de 208 y 59 años.
Indudablemente su valor de presión se alejó de la normal
para este grupo de estudio. Residual estudentizado le da entonces valores
alejados de la distribución de la variable dependiente. Qué
hacer? Eliminarlo? tiene que tener un argumento sólido para hacerlo...considere
previamente si es posible obtener un valor tan alejado de presión
sistólica.
REGRESIÓN MULTIPLE
Muchas veces hemos reunido múltiples variables, ojalá fueran
intervalares muchas de ellas, y con distribución normal, pero también
tenemos mezclas de variables nominales, ordinales e intervalares y debemos
analizar para esto puede servirnos regresión múltiple. En
el caso más sencillo de regresión múltiple nosotros
podemos tratar de predecir el valor de una variable dependiente a partir
de valores de dos o más variables independientes. La variable dependiente
en estos casos le llaman en inglés "outcome" (desenlace), y
las independientes son denominadas predictoras o covariables. No necesariamente
todas las variables predictoras deben ser continuas o intervalares.
Supongamos que deseamos predecir un índice de fuerza respiratoria
(Fresp, en cm H20) de acuerdo a la altura (en cm), al peso (en K), obtenemos
un modelo de regresión que dice:
Fresp = 47,35 + 0,147 (altura) + 1,024 (peso)
Los números 0,147 y 1,024 son los coeficientes de regresión
para la altura y el peso. 47,35 es la constante y dice que si altura y peso
son iguales a 0 la fuerza respiratoria va a ser de 47,35. Este valor no
es de mucha utilidad al igual que el intercepto que veiamos antes en regresión
simple.
En base a los analisis estadístico podemos obtener el error estándar
para cada coeficiente, calcular la significancia estadística de una
variable e intervalo de confianza para el coeficiente de regresión,
y cada pendiente puede ser significativa (o sea distinta de 0). Al igual que
en regresión simple se puede calculara anova y nos va a indicar que
tan bien el modelo sirve para esos datos.
Si en el modelo de regresión se incluye una variable binaria (debe
estar codificada 0 y 1, por ejemplo para sexo, mujer (0), hombre (1); también
en la misma forma no fumador y fumadores, etc) el coeficiente de regresión
para esta variable indica la diferencia promedio en la variable dependiente
entre los grupos definidos por la variable binaria, ajustada para cualquier
diferencia entre los grupos con respecto a las otras variables en el modelo.
A veces podemos incluir variables categóricas con más de dos
categorías, por ejemplo estado marital: que esté codificado
1 casado, 2 soltero, 3 viudo, o separado o divorciado. Si vamos a colocar
esta variable en el análisis de regresión (EST_MARITAL), se
estaría asumiendo una relación lineal que es falsa con códigos
1, 2, y 3, y esto se soluciona creando dos variables binarias, por ejemplo
definidas así:
MARIT_1: codificar 1 soltero; 0 cualquier otro;
MARIT_2: codificar 1 divorciado, viudo o separado; 0 cualquier otro.