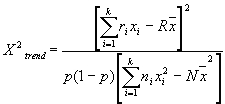
UNIDAD DE AUTO APRENDIZAJE
para alumnos de Odontología,
curso de Bioestadística.
ESTADISTICA NO PARAMÉTRICA
Dr. Benjamín Martínez R.
Profesor de Bioestadística
INTRODUCCIÓN
Afortunadamente para el estudio de la estadística no paramétrica se necesita conocimientos muy básicos de matemáticas y de estadística descriptiva, por lo que creemos que todos los tests estadísticos tratados en esta unidad son de fácil comprensión para un estudiante de odontología, y son tests que hemos incluído ya que puede requerir en análisis e interpretación de resultados de algún trabajo de investigación que realice durante sus estudios.
La estadística descriptiva utiliza la distribución normal o Gaussiana, con dos parámetros básicos promedio y desviación estándar, y esto se utiliza en variables o mediciones continuas. Pero muchas veces tenemos distribuciones Binomiales, asociadas con ciertos recuentos, y con dos parámetros n, y p, donde n es el número total de observaciones y p es la probabilidad que ocurra un evento para cada observación. El número total de ocurrencias r, tiene una distribución binomial en las n observaciones, 0<= r <= n.
La distribución binomial es relevante para conteos de eventos favorables. Esto se le llama generalmente "éxitos", pero puede ser aplicada esta distribución a situaciones dicotómicas. Por ejemplo el número de niños hombres en una familia de tamaño n tiene una distribución binomial con p = 1/2; también el número de seis registrados tirando 10 veces un dado tiene distribución binomial con n = 10 y p = 1/6.
Los test no paramétricos son menos fuertes o poderosos que los tests paramétricos (test de Student, ANOVA, análisis de regresión), pero deben aplicarse ya que son los únicos disponibles para datos que se han evaluado en orden (por ejemplo variables ordinales: grado de dolor evaluado como ausente, leve, moderado, marcado); rangos, o conteos de varias categorías.
Ejercicio 1.
1.- Frecuencia similar. ¿Está el dado
cargado ?
| Cara | f(0) | f(E) | (0-E)2/E |
| 1 | 7 | 10 | 0,9 |
| 2 | 5 | 10 | 2,5 |
| 3 | 15 | 10 | 2,5 |
| 4 | 17 | 10 | 4,9 |
| 5 | 5 | 10 | 2,5 |
| 6 | 11 | 10 | 0,1 |
| TOTAL | 60 | 60 | 13,40= c2 |
GL (grados de libertad) = 6 - 1 = 5 (número de filas - 1)
c2 0.05
= 11.07 (Valor crítico obtenido de la tabla de valores de c2). Aceptar H1.
El dado estaba cargado!!!
Ejercicio 2
2.- Se obtienen 200 números entre 0 y 9 de una
tabla de números aleatorios y se desea establecer si están bien
"aleatorios".
| Número | f(O) | f(E) | (0-E)2 /E |
| 0 | 21 | 20 | 0,05 |
| 1 | 20 | 20 | 0,00 |
| 2 | 22 | 20 | 0,20 |
| 3 | 20 | 20 | 0,00 |
| 4 | 27 | 20 | 2,45 |
| 5 | 16 | 20 | 0,80 |
| 6 | 23 | 20 | 0,20 |
| 7 | 13 | 20 | 2,45 |
| 8 | 17 | 20 | 0,45 |
| 9 | 22 | 20 | 0,20 |
| TOTAL | 200 | 200 | å = 6,80 = c2 |
c2 0.05 = 16.919 (valor crítico de la tabla de valores de c2 )
No significativo. El valor obtenido de 6,80 es menor que el crítico. Qué significa que no es significativo?
3.- Se evaluó en 300 ratas el efecto anti-cálculo de 3 pastas dentales habiéndose evaluado los depósitos como bajo, moderado, alto.
| Pasta Dental | Bajo (E) | Moderado (E) | Alto (E) | Total |
| A | 49 (55) | 30 (26) | 21 (19) | 100 |
| B | 67 (55) | 21 (26) | 12 (19) | 100 |
| C | 49 (55) | 27 (26) | 24 (19) | 100 |
|
TOTAL
|
165 | 78 | 57 | 300 |
El valor Esperado de la celda Bajo con Pasta Dental A se obtuvo:
E = (100 * 165) / 300 (ó en otras palabras: total de la fila por total de la columna divido por total de casos.
c2 = å(49 - 55)2/55 + ... + (24 - 19)2/19 = 9,65
gl = (f - 1) (c - 1) = (3 - 1) (3 - 1) = 4
(gl: grados de libertad, número de filas menos una, por número de columnas menos una).
c2 0.05 = 9,49 . Valor de chi cuadrado crítico. Interprete los resultados.
4.- Se observó que las edades en que se presentaba
un tumor (carcinoma espino celular del paladar) tenían esta distribución,
es normal ?
| Grupo de Edad (años) | f(0) | f(E) | (0 - E)2 /E |
| < 39 | 14 | 8,81 | 3,06 |
| 40 - 49 | 5 | 7,79 | 1,00 |
| 50 - 59 | 6 | 10,93 | 2,22 |
| 60 - 69 | 8 | 13,36 | 2,15 |
| 70 - 79 | 10 | 14,79 | 1,49 |
| 80 - 89 | 16 | 12,25 | 1,47 |
| 90 y más | 32 | 32,02 | 4,52 |
|
TOTAL
|
91 | 90,99 | 15,91= c2 |
En esta Tabla la frecuencia esperada debe obtenerse mediante m y d para estos datos:
m = 72.74
d = 25.5
Valores esperados :
Z= (x - m)/ d = (39,5 – 72,74)/25,5 = 1,30
Z1.30 = 0,4032 (de tabla de valores de Z)
0.5 - 0,4032 = 0,0968
0,0968 * 91= 8.808 (Valor que aparece en
la tabla como 8,81. Trate de calcular los otros valores de frecuencias esperadas.
Chi-cuadrado es un test estadístico que indica si dos variables son o no independientes y NO entrega información acerca de la fuerza, dirección, o patrón de la asociación que pudiera haber entre ellas. El cálculo de este estadístico está basado en la relación entre las frecuencias en celdas que observamos en una tabla construída previamente (frecuencias observadas) y las frecuencias que esperamos observar, si se cumple como verdadera la hipótesis nula de que no hay asociación entre las variables.
c2 de Pearson = å (O - E)2 / E
c2 con corrección de Yates = å( |O - E| - 1/2)2 / E
La corrección de Yates es solamente para tablas 2x2 y con muestras pequeñas, o sea cuando en una celda existan menos de cinco observaciones. El tamaño ideal para realizar el test de chi-cuadrado debe calcularse multiplicando por 10 el número de celdas, por ejemplo para una tabla de 2x2 el ideal debiera ser 40 casos. No calcule el tamaño de la muestra cuando está por terminar la investigación, esto debe haberlo realizado cuando escribió el protocolo y había (ó debería) pensado en qué análsis realizar.
El análisis de dos variables categóricas trata de determinar una relación, o sea asociación entre dos variables. La mejor forma de evaluar la asociación entre dos variables es calcular los porcentajes, pero de todas formas se necesita resumir esto en forma concisa. Cuando pensamos como resumir una asociación hay cuatro características que debemos tener en cuenta:
Lambda de Goodman y Kruskal constituyen una medida de la existencia y de la fuerza de la asociación entre dos variables y varía entre 0 y 1. Lambda es 1 cuando para cada categoría de la variable independiente, solamente una celda de la tabla contiene todos los casos. O sea en este caso conociendo el valor de la variable independiente le permite hacer una predicción perfecta de la variable dependiente (una reducción del error en 100%). Cuando tenemos que dos variables son estadísticamente independientes, lambda es cero. Desgraciadamente lo contrario no es verdadero, cuando lambda es cero no significa que las dos variables son independientes. Lambda debe usarse para variables nominales. En el caso de variables ordinales debe utilizar otras mediciones. Lambda y otras mediciones son calculadas por la mayoría de los softwares estadísticos.
Medidas para asociación de variables ordinales.
Existen dos diferencias con las medidas de asociación que se usan
en variables nominales. Primero, debido a que las categorías están
ordenadas, la asociación entre dos variables tiene una dirección
indicada por el signo del coeficiente. Un signo más indica asociación
positiva, el signo menos indica asociación inversa (similar a lo que
ocurre con la correlación de Pearson), por lo que el valor va entre
1.0 y -1.0 pasando por 0 que indica ausencia de asociación y 1 asociación
perfecta positiva. Segundo, debido a que las categorías están
ordenadas los casos pueden ser ranqueados de acuerdo a si caen en categorías
más altas o más bajas (Wilkinson).
Para las tablas ordinales la medida más utilizada se denomina Gamma de Goodman y Kruskal, además es la más simple. Se preocupa de contar solamente pares concordantes y discordantes en su fórmula (concordantes: aquellos pares serán concordantes cuando están ranqueados en el mismo orden en ambas variables, y discordantes son ranqueados en orden opuesto en ambas variables).
concordancias - discordancias
g = ----------------------------------------
concordancias + discordancias
Gamma es una medida simétrica de asociación. Esto
significa que tiene el mismo valor indistintamente si la variable independiente
es la variable en las filas o las columnas. Dado que gamma no incluye ningún
par empatado puede basarse en un número pequeño de casos. En
el hecho, gamma puede ser 1 (ó -1) basado solamente en un par si todos
los otros pares estaban empatados en una o ambas variables. En las tablas
de 2x2 a gamma se le llama Q de Yule y la mayoría de los softwares
estadísticos también entregan este valor.
Chi cuadrado se utiliza mucho más que en los ejemplos anteriores en
tablas de contingencia de 2 x 2, por ejemplo si tenemos:
| Mejoró | No Mejoró | TOTAL | |
| Droga | 48 | 8 | 56 |
| Placebo | 38 | 13 | 51 |
| TOTAL | 86 | 21 | 107 |
| Mejoró | No Mejoró | TOTAL | |
| Droga | a | b | a + b |
| Placeo | c | d | c + d |
| TOTAL | a + c | b + d | a+b+c+d |
Aplicando:
c2 con corrección de Yates = å( |O - E| - 1/2)2 / E
Obtenemos:
c2 = (|48 - 45,01| - 0,5)2 /45,01 + (|8 - 10,99| - 0,5)2 /10,99 + (|38 - 40,99| - 0,5)2 / 40,99 +
(|13 - 10,01| - 0,5)2 / 10,01
c2 = 0,138 + 0,564 + 0,151 + 0,619 = 1,47
Grados de libertad (nf - 1) (nc - 1) = (2 - 1)(2-1) = 1
De acuerdo a la tabla de valores críticos para chi cuadrado con 1 grado de libertad y para p<0,05 = 3,84. Por lo tanto afirmamos que no existen diferencias significativas. O en otras palabras la mejoría fue similar con droga o placebo.
Muchas veces en las tablas de 2 x 2 se calcula el odds ratio que se refiere
a la relación de frecuencias de dos categorías y también
se conoce o es equivalente al riesgo relativo. De acuerdo a la tabla con
las celdas a, b, c y d, el odds ratiio se calcula:
OR = a/b - c/d
Cuando OR es mayor que uno, un sujeto en la fila uno es más (o menos)
probable de ser clasificado en la columna uno que un sujeto en la fila dos.
Con un OR de uno, queremos decir que no hay asociación, y este valor
puede ir de cero a infinito, y entre más alejado de uno indica una
fuerte asociación.
El logaritmo de OR (Ln(Odds)) puede utilizarse para tests de significancia
estadística y construir intervalos de confianza para el OR, con un
rango entre 0 e infinito.Con el OR, el Ln y el error estándar que
entregan la mayoría de los softwares estadísticos se puede
calcular el intervalo de confianza para el OR.
Analice los resultados de la misma tabla obtenidos con software estadístico
SYSTAT Output
File D:\PATOLOGIA\BIOESTADISTICA\TABLA.SYD
SYSTAT Rectangular
file D:\PATOLOGIA\bioestadistica\Tabla.syd,
Two-way Tables - Statistics
Cases are
weighted by the value of variable N.
Frequencies
GRUPO$ (rows)
by RESP_$ (columns)
| MEJOR | NO MEJOR | Total | |
| DROGA | 48.000 | 8.000 | 56.000 |
| PLACEBO | 38.000 | 13.000 | 51.000 |
| Total | 86.000 | 21.000 | 107.000 |
Row percents
GRUPO$ (rows)
by RESP_$ (columns)
| MEJOR | NO MEJOR | Total | N | |
| DROGA | 85.714 | 14.286 | 100.000 | 56.000 |
| PLACEBO | 74.510 | 25.490 | 100.000 | 51.000 |
| Total | 80.374 | 19.626 | 100.000 | |
| N | 86.000 | 21.000 | 107.000 |
| Test statistic | Value | df | Prob |
| Pearson Chi-square | 2.124 | 1.000 | 0.145 |
| Yates corrected Chi-square | 1.473 | 1.000 | 0.225 |
| Fisher exact test (two-tail) | 0.223 |
| Coefficient | Value | Asymptotic Std Error |
| Odds Ratio | 2.053 | |
| Ln(Odds) | 0.719 | 0.499 |
| Yule Q | 0.345 | 0.220 |
| Yule Y | 0.178 | 0.121 |
Conteste las siguientes preguntas:
1. Por qué existe diferencia en el valor de chi-cuadrado con y sin
corrección de Yates?
2. Los porcentajes de mejoría como son?
3. Qué significa la Q de Yule de 0,345?
4. En la última tabla aparece Odds Ratio = 2,053 Sabe ud. para qué
sirve ? También para qué sirve el valor que dice Ln(Odds) =
0,719, con error estándar asintótico de 0,499?
Muchas veces necesitamos evaluar en variables ordinales o con categorías que siguen un orden si existe una tendencia, para esto nos sirve este test de chi-cuadrado cuya formula es:
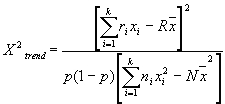
Ejemplo tomado del libro de Altman, página 263, en donde se quiere
ver la relación de frecuencia de cesáreas y zapato materno
(Frame, y col., 1985). Yo habría visto relación entre cáncer
oral vs. Años en hombres y mujeres u otra tendencia más estimulante,
pero nos limitamos al ejemplo:
| |
Tamañodel zapato (talla Inglesa, por ejemplo 5 equivale a 37) | ||||||
| Cesárea | <4 | 4 | 4 1/2 | 5 |
5 1/2 | 6 + |
Total |
| Si | 5 | 7 | 6 | 7 | 8 | 10 | 43 |
| No | 17 | 28 | 36 | 41 | 46 | 140 | 308 |
| Total | 22 | 35 | 42 | 48 | 54 | 150 | 351 |
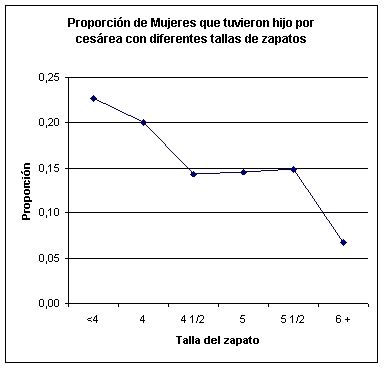
Fig. Proporciòn
de mujeres que tuvieron hijo por cesárea con diferentes tallas de
zapatos.
Para evaluar la tendencia lo que debemos hacer es encontrar si existe una línea que siga una inclinación o pendiente de acuerdo a los valores observados, en este caso las proporciones en cada grupo, o en otras palabras que porcentaje de mujeres que tuvieron cesárea, tenían cada talla de zapatos y lo que vamos a demostrar es si la pendiente es distinta de 0 (igual que en análisis de regresión simple).
Tabla. Datos de Tamaño de zapato materno y frecuencia de cesárea
(Frame et al, Brit J obst Gynaecol92;1239, 1985)
| |
Tamaño del zapato (talla Inglesa, por ejemplo 5 equivale a 37) | |||||||
| Cesárea | <4 | 4 | 4 1/2 | 5 |
5 1/2 | 6 + |
Total |
|
| Si (ri) | 5 |
7 |
6 |
7 | 8 |
10 |
43 ( = R) |
|
| Total (ni) | 22 |
35 | 42 |
48 |
54 |
150 |
351 ( = N) | |
| Score (xi) | 1 |
2 |
3 |
4 |
5 |
6 |
||
(rixi) |
5 |
14 |
18 |
28 |
40 |
60 |
165 |
|
(nixi) |
22 |
70 |
126 |
192 |
270 |
900 |
1580 |
|
(nix2i) |
22 |
140 |
378 |
768 |
1350 |
5400 |
8058 |
|
Promedio (x) = 1580 / 351 = 4,5014; p = 43 / 351 = 0,1225; 1 – p = 0,8775
El score 1 a 6 se dá de acuerdo al orden de la tabla, o en este caso desde la talla menor (<4) hasta la más grande 6 +.
![]()
![]()
Si se calcula el valor de chi-cuadrado
en la forma tradicional explicada anteriormente se obtiene 9,29 y con 5 grados
de libertad, el cual no es significativo (p = 0,098), pero si se considera
acá que los grados de libertad son solamente uno (ya que se toma en
cuenta el número de variables menos 1) se obtiene que p < 0,05.
Por lo tanto podemos afirmar que existe fuerte tendencia linear que
una proporción de mujeres tienen cesárea de acuerdo al tamaño
o talla del zapato (!), pero esto no es lo mismo a tratar de predecir qué
mujeres de qué talla de zapato van a tener que ir a cesárea.
Tabla de Valores de chi-cuadrado
| Grados de Libertad | 0,05 | 0,01 |
| 1 | 3,84 | 6,63 |
| 2 | 5,99 | 9,21 |
| 3 | 7,81 | 11,34 |
| 4 | 9,49 | 13,28 |
| 5 | 11,07 | 15,09 |
| 6 | 12,59 | 16,81 |
| 7 | 14,07 | 18,48 |
| 8 | 15,51 | 20,09 |
| 9 | 16,92 | 21,67 |
| 10 | 18,31 | 23,21 |
| 11 | 19,68 | 24,72 |
| 12 | 21,03 | 26,22 |
| 13 | 22,36 | 27,69 |
| 14 | 23,68 | 29,14 |
| 15 | 25,00 | 30,58 |
| 16 | 26,30 | 32,00 |
| 17 | 27,59 | 33,41 |
| 18 | 28,87 | 34,81 |
| 19 | 30,14 | 36,19 |
| 20 | 31,41 | 37,57 |
| 21 | 32,67 | 38,93 |
| 22 | 33,92 | 40,29 |
| 23 | 35,17 | 41,64 |
| 24 | 36,42 | 42,98 |
| 25 | 37,65 | 44,31 |
| 26 | 38,89 | 45,64 |
| 27 | 40,11 | 46,96 |
| 28 | 41,34 | 48,28 |
| 29 | 42,56 | 49,59 |
| 30 | 43,77 | 50,89 |
| 40 | 55,76 | 63,69 |
| 50 | 67,50 | 76,15 |
| 60 | 79,08 | 88,38 |
| 70 | 90,53 | 100,42 |
| 80 | 101,88 | 112,33 |
| 90 | 113,14 | 124,12 |
| 100 | 124,34 | 135,81 |
Test del signo del Rango.
Este test es equivalente al test t pareado o sea para
comparaciones antes y después de un tratamiento, pero aquí tenemos
variables que no siguen una distribución normal o que son ordinales.
Se evaluó el efecto de un diurético, producción
de orina mL/día. (Antes y Después se refiere al valor
obtenido en mL/día de orina antes y despueés de administrado
el diurético).
| Pcte | Antes | Después | Diferencia | Rango de la dif. * |
Signo del Rango |
| 1 | 1600 | 1490 | -110 | 5 | -5 |
| 2 | 1850 | 1300 | -550 | 6 | -6 |
| 3 | 1300 | 1400 | 100 | 4 | 4 |
| 4 | 1500 | 1410 | -90 | 3 | -3 |
| 5 | 1400 | 1350 | -50 | 2 | -2 |
| 6 | 1010 | 1000 | -10 | 1 | -1 |
| W = - 13 |
7.- Test de Mann-Whitney
Este test es equivalente al test t no pareado.
Producción de orina diaria mL/día en dos
grupos de pacientes, a los cuales se les administró placebo y al otro
grupo droga diurética.
| Placebo | Rango | Droga | Rango |
| 1000 | 1 | 1400 | 6 |
| 1380 | 5 | 1600 | 7 |
| 1200 | 3 | 1180 | 2 |
| 1220 | 4 | ||
|
T =
|
9 | 19 |
Mann-Whitney U = 9, p = 0.289. (Valor de p obtenido del análisis realizado con Systat. Si ud. no tiene software estadístico debe ubicar en libro de estadística, como los que figuran en las referencias, la tabla de valores para el test de Mann-Whitney).
Resultado con Systat:
Categorical values encountered during
processing are:
GRUPO$ (2 levels)
droga, p
Kruskal-Wallis One-Way Analysis of Variance for 7 cases
Dependent variable is ORINA
Grouping variable is GRUPO$
Group Count
Rank Sum
droga
4 19.000
p
3 9.000
Mann-Whitney U test statistic =
9.000
Probability is 0.289
Chi-square approximation = 1.125
with 1 df.
N = Sini.
Obtenemos rango de todas las
observaciones N desde la más pequeña (rango 1) a la
más grande (rango N), rangos empatados se da el promedio del
valor que corresponda.
Si tenemos rij
el rango asignado a xi,j y si, = Sjrij
la suma de los rangos para la muestra i.
Calculamos:
Sp = Si ( si2 / ni ) y
Sr = Si, jrij2
Esto corresponde a la suma
de cuadrados de rango para los tratamientos y del total, similar a lo que
veíamos en ANOVA. De cada uno de ellos sustraemos una corrección
apropiada para el promedio,
C =1/4 N ( N + 1 )2
Si no hay empates :
Sr = N ( N + 1 ) ( 2N +
1 ) / 6. El test estadístico es :
( n - 1) (Sp - C)
T = ---------------------
Sr - C
Sin empates se simplifica
a:
T = 12 Sp / [ N ( N + 1
)] - 3 ( N + 1 )
Si N es moderado o grande,
T tiene una aproximación a la distribución de chi-cuadrado con
p-1 grados de libertad si no hay diferencia en los tratamientos.
Ejemplo:
Se realizó recuento
de linfocitos en biopsias de pacientes controles (A), glándulas adyacentes
a Mucoceles (B), y en pacientes con Síndrome de Sjögren (C),
| Condición | Recuentos |
| A | 13 27 26 22 26 |
| B | 43 35 47 32 31 37 |
| C | 33 33 33 26 44 33 54 |
Es bueno ordenar los rangos
| Condición | Recuento |
| A R: |
13 22 26 26 27 1 2 4 4 6 |
| B R: |
31 32 35 37
43 47 7 8 12 13,5 15 17 |
| C R: |
26 33 33 33
37 44 54 4 10 10 10 13,5 16 18 |
s1= 1+ 2+ 4+ 4+6 = 17
s2= 7+ 8+ 12+ 13,5+ 15+ 17= 72,5
s3= 4+ 10+ 10+ 10+ 13,5+ 16+ 18= 81,5
sp= ( 17 )2/ 5+ ( 72,5 )2/ 6+ ( 81,5 )2/ 7= 1882,73
Suma de cuadrados de los rangos medios:
Sr = 2104,5
C = 18 x ( 19 )2/ 4
= 1624,5
T = 17 ( 1882,73 - 1624,5 ) / ( 2104,5 - 1624,5 )
= 9,146
Grados de libertad = 3 - 1= 2
Por lo tanto rechazamos la hipótesis de nulidad y el grupoA tiene un recuento de linfocitos menor, que difiere en forma significativa, o en otras palabras las glándulas salivales normales tenían menor recuento de linfocitos.
Comparaciones múltples después de realizado Kruskal - Wallis.
Si existen diferencias significativas debemos realizar la comparación
entre los grupos, o sea en el ejemplo anterior habría posibilidad de
determinar si existen diferencias significativas entre:
A vs B ( controles vs mucoceles)
A vs C (controles vs Sjögren)
B vs C (mucoeles vs Sjögren)
algo similar a lo que se hace con test de Scheffé o Tukey después
de realizar el ANOVA.
Si tenemos los promedios de los rangos para estas muestras:
| mi - mj | > tN-t,a [( Sr
- C ) ( N -1 -T ) ( ni + nj )/{ni nj ( N - T) ( N - 1) }]1/2
(recuerde que la expresión entre [ ... ]1/2
debe obtener la raíz cuadrada)
donde T es el valor encontrado y tn-t,a es el valor de t requerido para significancia al 100% del nivel de significancia en un test con N- t grados de libertad y los otros valores ya están descritos .
En el ejemplo anterior veíamos que el recuento en A era menor, debemos
determinar si difiere en forma significativa del que le sigue, o sea en B.
Los rangos que importan son :
m1 = 17/ 5 = 3,4 para A
m2 = 72,5 /5 = 12,1 para B
Grados de libeeertad : ( n1 - 1 ) + (
n2 - 1 ) + ( n3
- 1 ) = 15.
Tenemos Sr- C = 2104,5 - 1624,5= 480,0 y T = 9,146, N = 18, n1 = 5, n2 = 6,
t = 3 y de acuerdo a la tabla de valores críticos al 1% de significancia
con 15 grados de libertad, que es 2,95. Por lo que el lado izquierdo de la
fórmula anterior es 12,1 - 3,4 = 8,7, y el lado derecho es 2,95
[ ( 480 ) (17 - 9,164 ) ( 11 ) / 6 x 5 ( 17 ) ( 15 ) ]1/2
=6,86.
Ya que 8,7 > 6,86 la diferencia es significativa. O sea existen diferencias
entre el grupo A y B.
Si quiere entretenerse un poco, realice las comparaciones entre A vs. C y
B vs. C.
Correlación de Spearman
Equivalente del análisis de regresión pero para variables ordinales o para determinar la significancia de la asociación de dos variables continuas en que no existe normalidad de ellas. Contrapartida no paramétrica de la correlación de Pearson.
rs = 1 - 6å(xi – yi)2 /n(n2 – 1) = 1 – 6å d2 /(n – 1)(n)(n + 1) = 1 – 6å d2 /n3 – 1
(n: número de pares de obs.)
(xi – yi : diferencia en rango de x con
respecto a y)
Si tenemos un valor que corresponde a reabsorción de hueso en la mandíbula al lado derecho y deseamos establecer en 10 pacientes si es independiente de lo que ocurre al lado izquierdo, tenemos:
| Der | 83 | 97 | 91 | 72 | 76 | 88 | 95 | 89 | 75 | 74 |
|
Rango
|
|
|
|
|
|
|
|
|
|
|
| Izq | 87 | 98 | 84 | 82 | 74 | 92 | 91 | 83 | 80 | 77 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d2
|
|
|
|
|
|
|
|
|
|
|
rs = 1 – 6(40)/10(102 – 1) = 0,757
Para determinar si existe significancia estadística en el valor de correlación de Spearman (rs) es necesario calrcular valor de t, similar a lo que se realiza en la correlación de Pearson.
t = rs / [ (1 - rs2) / (N - 2)]1/2
[ ]1/2 Esta expresión, significa obtener raíz cuadrado
de lo encerrado en el paréntesis cuadrado.
Referencias Bibliográficas.